publications

* denotes equal contribution and joint lead authorship.
  1. Efficient variational computation of excitons and their optical properties using localized orbitals basis.
    Alejandro José Uría, Juan José Esteve-Paredes, and Juan José Palacios.

    In preparation (2022).

  2. A theoretical approach for electron dynamics and ultrafast spectroscopy.
    Giovanni Cistaro, Mikhail Malakhov, Juan José Esteve-Paredes, Alejandro José Uría-Álvarez, Rui E. F. Silva, Fernando Martín, Juan José Palacios, and Antonio Picón.

    In arXiv:2207.00249 (2022).

    HTML
    In this manuscript we present a theoretical framework and its numerical implementation to simulate the out-of-equilibrium electron dynamics induced by the interaction of ultrashort laser pulses in condensed-matter systems. Our approach is based on evolving in real-time the density matrix of the system in reciprocal space. It considers excitonic and non-perturbative light-matter interactions. We show some relevant examples that illustrate the efficiency and flexibility of the approach to describe realistic ultrafast spectroscopy experiments. Our approach is suitable for modeling the promising and emerging ultrafast studies at the attosecond time scale that aim at capturing the electron dynamics and the dynamical electron-electron correlations via X-ray absorption spectroscopy.
  3. Deep learning for disordered topological insulators through their entanglement spectrum.
    Alejandro José Uría-Álvarez, Daniel Molpeceres-Mingo, and Juan José Palacios.

    In Phys. Rev. B 105, 155128 (2022).

    HTML
    Calculation of topological invariants for crystalline systems is well understood in reciprocal space, allowing for the topological classification of a wide spectrum of materials. In this work, we present a technique based on the entanglement spectrum, which can be used to identify the hidden topology of systems without translational invariance. By training a neural network to distinguish between trivial and topological phases using the entanglement spectrum obtained from crystalline or weakly disordered phases, we can predict the topological phase diagram for generic disordered systems. This approach becomes particularly useful for gapless systems, while providing a computational speed-up compared to the commonly used Wilson loop technique for gapful situations. Our methodology is illustrated in two-dimensional models based on the Wilson-Dirac lattice Hamiltonian.

2022

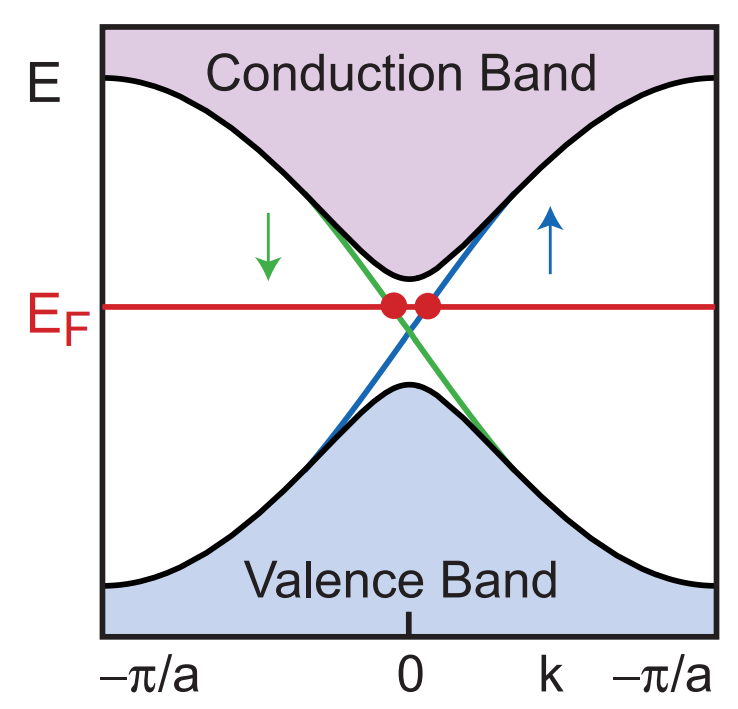
  1. Materia topológica: aislantes.
    Alejandro José Uría Álvarez.

    In Undergrad physics thesis (2017).

    HTML
    Una de las principales áreas de interés de la física de la materia condensada es aquella centrada en el estudio de las propiedades de transporte electrónico de los distintos materiales, dando lugar a una clasificación bien conocida: metales, semiconductores y aislantes. Mientras que los dos primeros son sobradamente conocidos, los aislantes carecían de interés teórico hasta la fecha, con la predicción y descubrimiento de unos materiales exóticos que poseen una estructura de bandas análoga a la de un aislante, pero exhibiendo una conductividad no nula: los aislantes topológicos.

2017